Mastering Consecutive Angles: An Essential Guide for Mathematics Enthusiasts
Mathematics, in its elegant simplicity, often relies on the precise understanding of fundamental concepts. Among these, the concept of consecutive angles stands as a cornerstone, particularly in geometry and trigonometry. Whether you’re a student grappling with proofs or a seasoned enthusiast seeking to deepen your knowledge, mastering consecutive angles is crucial for unlocking the full potential of mathematical problem-solving. This article serves as a comprehensive guide to understanding, identifying, and applying the principles of consecutive angles. We’ll break down the concepts, providing clear examples and practical applications to solidify your understanding.
What are Consecutive Angles?
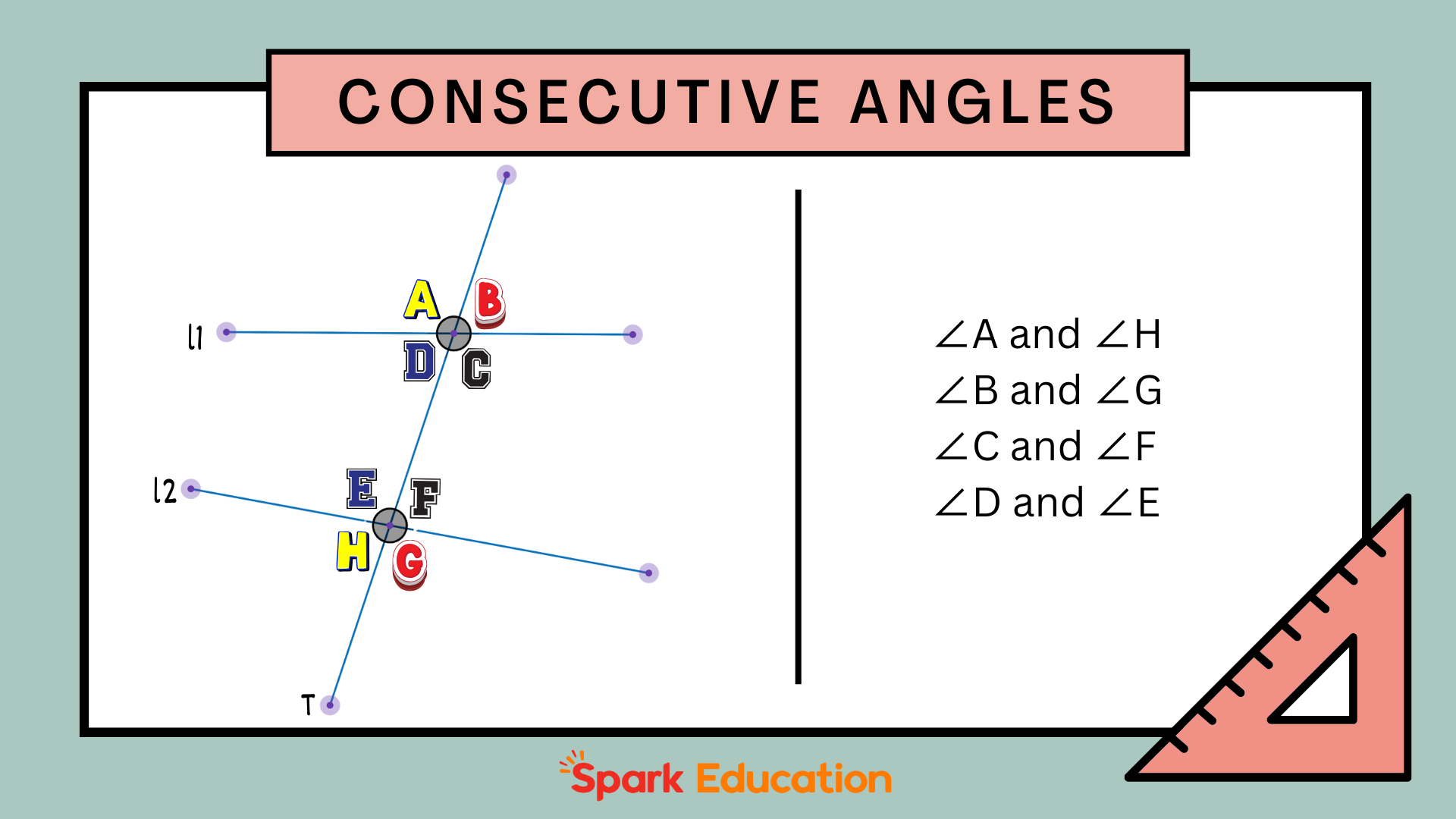
At its core, the term “consecutive” in mathematics implies a sequence or order. In the context of angles, consecutive angles refer to angles that follow each other in a specific sequence, typically around a point or along a line. They share a common vertex and a common side, and are adjacent to each other. Understanding this adjacency is key to grasping their relationships and properties.
Types of Consecutive Angles and Their Properties
There are several key types of consecutive angles you’ll encounter in your mathematical explorations:
- Angles on a Straight Line: These are consecutive angles that lie on the same straight line. The most important property here is that the sum of these angles always equals 180 degrees (a straight angle).
- Example: If you have three consecutive angles on a straight line, labelled A, B, and C, then: Angle A + Angle B + Angle C = 180°
- Angles Around a Point: These are consecutive angles that share a common vertex (a point) and form a complete revolution around that point. The sum of these angles always equals 360 degrees.
- Example: Imagine four consecutive angles surrounding a point, labelled P, Q, R, and S. Then: Angle P + Angle Q + Angle R + Angle S = 360°
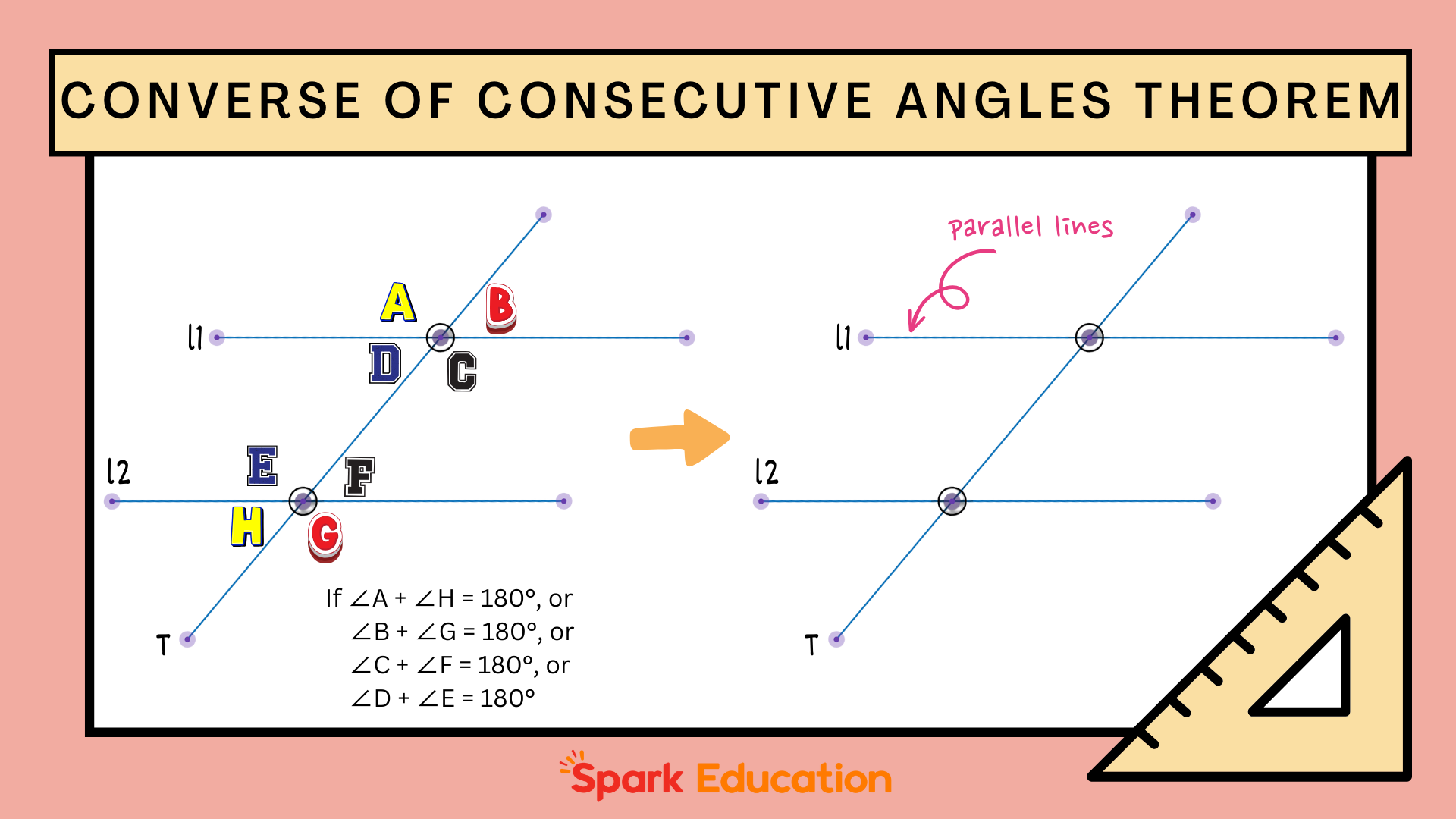
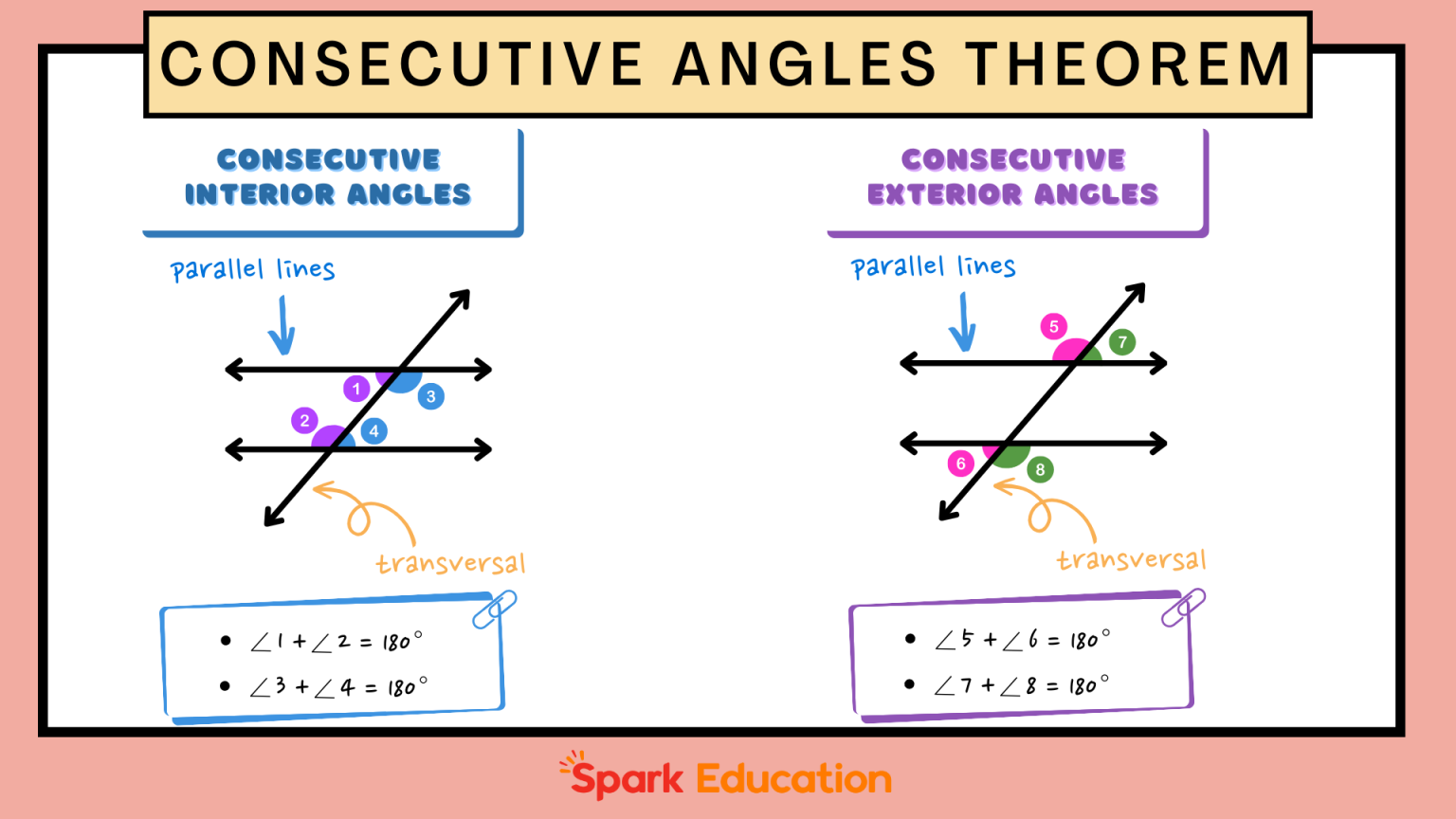
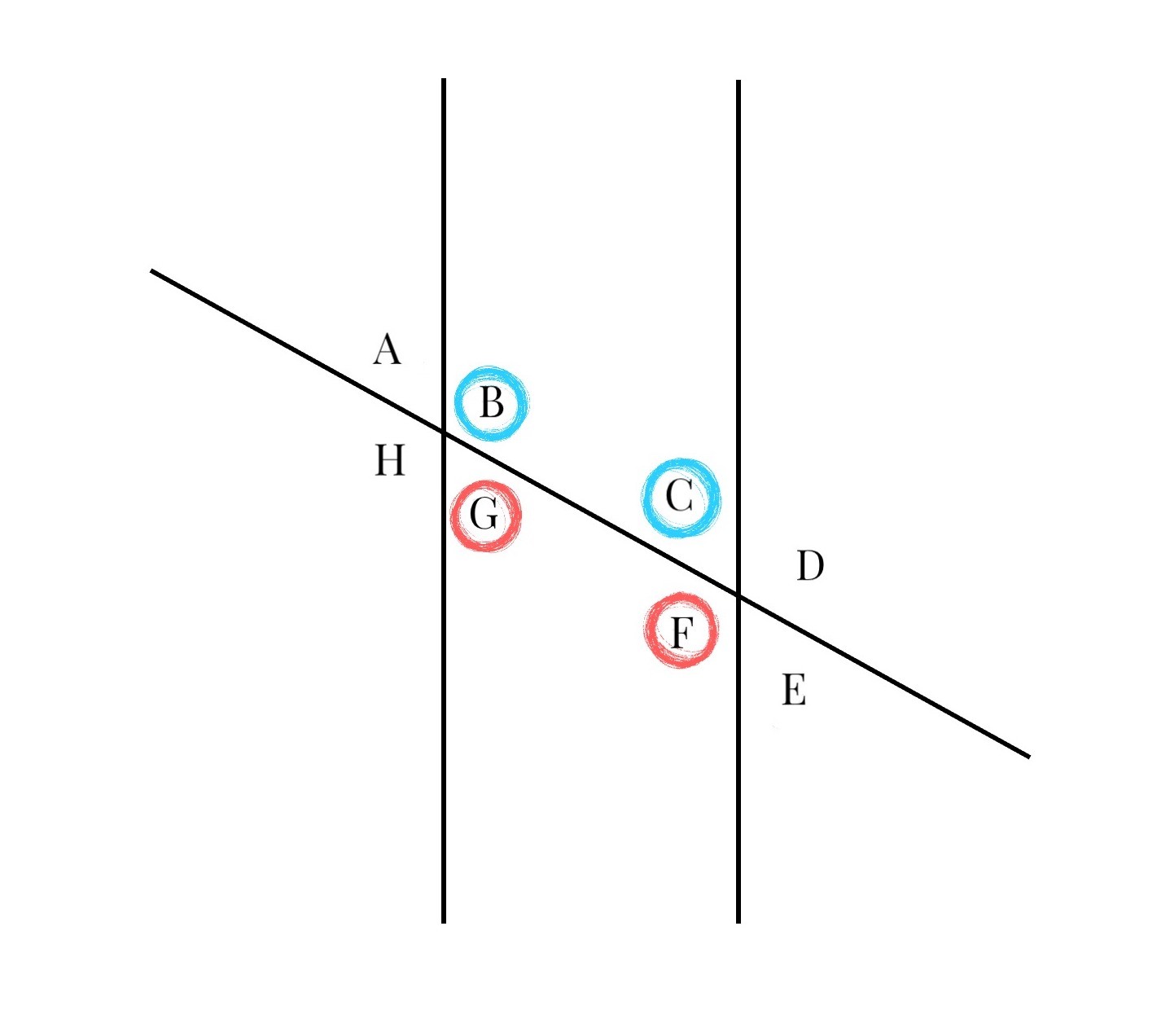
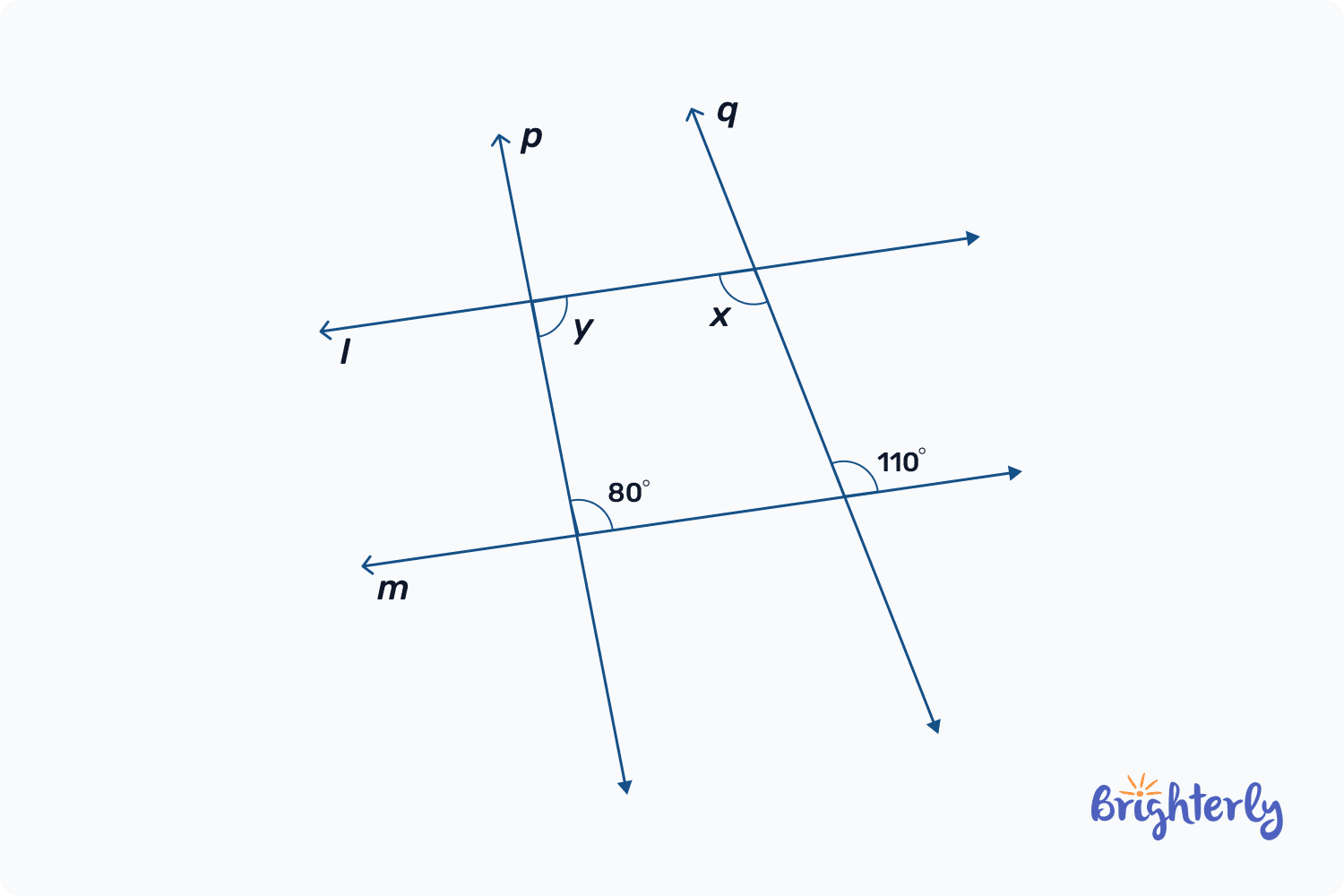
- Consecutive Interior Angles (Same-Side Interior Angles): These angles are formed when a transversal intersects two parallel lines. They are located on the same side of the transversal and inside the parallel lines.
- Key Property: The sum of consecutive interior angles is always 180 degrees. This is a critical concept in proving theorems about parallel lines.
- Consecutive Exterior Angles (Same-Side Exterior Angles): Similar to consecutive interior angles, these angles are formed by a transversal intersecting two parallel lines. They lie on the same side of the transversal, but outside the parallel lines.
- Key Property: The sum of consecutive exterior angles is also 180 degrees.
Identifying and Applying Consecutive Angle Relationships
The ability to identify consecutive angles and apply their properties is essential for solving geometric problems. Here’s a step-by-step approach:
- Visualize the Situation: Carefully examine the diagram or problem description. Identify the angles in question and their spatial relationship.
- Determine the Type: Determine whether you’re dealing with angles on a straight line, angles around a point, or angles formed by parallel lines and a transversal.
- Apply the Relevant Property: Based on the type of consecutive angles, apply the corresponding property (sum of 180° or 360°) to set up an equation.
- Solve the Equation: Use algebraic techniques to solve for the unknown angle(s).
- Verify Your Solution: Check your answer to ensure it makes sense in the context of the problem.
Examples and Practical Applications
- Example 1: Finding a Missing Angle on a Straight Line:
- Problem: Two consecutive angles on a straight line measure 60° and x°. Find the value of x.
- Solution: Since the angles are on a straight line, their sum is 180°. Therefore, 60° + x° = 180°. Solving for x, we get x = 120°.
- Example 2: Calculating an Angle Around a Point:
- Problem: Three consecutive angles around a point measure 100°, 130°, and y°. Find the value of y.
- Solution: The sum of angles around a point is 360°. Therefore, 100° + 130° + y° = 360°. Solving for y, we get y = 130°.
- Practical Application: Architectural Design: Architects use angle relationships, including consecutive angles, to design structures that are stable and aesthetically pleasing. Understanding these relationships is crucial for calculating the angles needed for walls, roofs, and other architectural elements.
- Practical Application: Navigation and Surveying: Surveyors and navigators rely heavily on angle measurements, including consecutive angles, to determine distances, directions, and locations.
Mastering Consecutive Angles: Tips for Success
- Practice Regularly: The more you practice solving problems involving consecutive angles, the more comfortable you’ll become with the concepts.
- Draw Diagrams: Always draw a clear diagram to visualize the problem. This will help you identify the angles and their relationships.
- Review Key Properties: Familiarize yourself with the properties of each type of consecutive angle.
- Seek Help When Needed: Don’t hesitate to ask your teacher, tutor, or classmates for help if you’re struggling with a particular concept.
- Explore Real-World Examples: Look for examples of consecutive angles in the world around you, such as in buildings, furniture, and artwork.
Conclusion
Mastering consecutive angles is a fundamental step in your journey through mathematics. By understanding the definitions, properties, and applications of these angles, you’ll be well-equipped to tackle more complex geometric problems and deepen your appreciation for the beauty and elegance of mathematics. Consistent practice and a solid grasp of the principles outlined in this guide will pave the way for your success.
Frequently Asked Questions (FAQs)
- What is the difference between adjacent angles and consecutive angles?
- Adjacent angles share a common vertex and a common side, but the term “consecutive” implies a specific order or sequence. Consecutive angles are always adjacent, but not all adjacent angles are consecutive.
- Do the angles have to be next to each other to be consecutive?
- Yes, by definition, consecutive angles must be adjacent to each other, sharing a common vertex and side, and following each other in a sequence.
- How do I know if lines are parallel?
- Lines are considered parallel if they never intersect, no matter how far they are extended. You can also use angle relationships (like equal corresponding angles or supplementary consecutive interior angles) to determine if lines are parallel.
- Can consecutive angles be obtuse?
- Yes, consecutive angles can be obtuse, depending on the specific situation. For example, in angles around a point, you can have several obtuse angles that are consecutive. Similarly, an obtuse angle can exist as part of consecutive angles on a straight line.
- What is the relationship between consecutive interior angles and parallel lines?
- When a transversal intersects two parallel lines, the consecutive interior angles are supplementary (they add up to 180 degrees). Conversely, if the consecutive interior angles formed by a transversal and two lines are supplementary, then the lines are parallel.